VALOR ABSOLUTO DE UN NUMERO REAL

Valor absoluto de un número real

Cualquier número a tiene su representación en la recta real. El valor absoluto de un número representa la distancia desde ese número al origen.

Observe en el dibujo que la distancia del 6 al origen es 6 unidades, igualmente la distancia del punto −6 al origen es 6. En notación, esto es |−6| = 6 .

Las barras se leen como el valor absoluto de lo que esta dentro de ellas.

En el valor absoluto no importa en que lado de la recta real está representado el número.

De modo general, el valor absoluto de un número real a , se escribe |a| , es el mismo número a cuando es positivo o cero , y opuesto de a , si a es negativo .

Analíticamente podemos ver que si a es positivo, es decir esta a la derecha del cero, entonces |a| = a y si está a la izquierda del origen, es decir si a es negativo, entonces | a| = −a .

Formalmente, el valor absoluto o módulo de todo número real |a| está definido por:

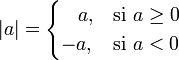
Por definición, el valor absoluto de |a| siempre será mayor o igual que cero y nunca negativo.

Desde un punto de vista geométrico, el valor absoluto de un número real |a| es siempre positivo o cero, pero nunca negativo.

En general, el valor absoluto de la diferencia de dos números reales |a − b| es la distancia entre ellos.

Veamos los siguientes ejemplos

Ejemplo 1

a)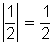 

b)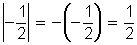 

Observe como el valor absoluto a una cantidad positiva la deja igual y a una cantidad negativa le cambia el signo.

c) Si x > 2 entonces | x – 2| = x – 2 , pues x − 2 > 0 . Dicho de otra manera, si la expresión a la que le estamos tomando valor absoluto es de signo positivo, el valor absoluto la deja igual.

d) Si x < 2 entonces |x – 2| = – (x – 2) ,  pues x − 2 < 0 . Dicho de otro modo, si la expresión a la que le estamos tomando valor absoluto es de signo negativo, el valor absoluto la cambia de signo.

Ecuaciones con valor absoluto

Si x es una incógnita en la expresión |x − 3| , entonces no sabemos si x − 3 es positivo o negativo. Ahora bien, si tenemos la ecuación:

|x − 3| = 5

deberíamos considerar las dos posibilidades de signo. Es decir hay dos alternativas:

x − 3 = 5

o bien

x − 3 = −5
La primera es en el caso de que x − 3 sea positivo, la segunda en la situación de que sea negativo.

Resolviendo las dos ecuación, tenemos que

x = 8 o bien x = −2

Efectivamente, estos valores de x satisfacen la ecuación: |x − 3| = 5

Veamos más ejemplos de resolución de ecuaciones en valor absoluto

Resolver |x − 4| = 3

Hay dos posibilidades: x − 4 = 3 o bien x − 4 = −3 .

Las soluciones de ellas son 7 y 1 .

Veamos:

x − 4 = 3

x = 3 + 4

x = 7

o bien

x − 4 = −3

x = −3 + 4

x = 1

Resolver 3 |5 − 4x| = 9

Veamos:

Hasta ahora, sabemos resolver una ecuación con valor absoluto cuando el valor absoluto se presenta en el lado izquierdo, así es que lo llevamos a esta forma, dividiendo entre 3 ambos miembros de la ecuación:

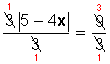
De esta manera la ecuación dada es equivalente a:

|5 − 4x| = 3

Ahora,  esta ecuación en valor absoluto es equivalente a

5 − 4x = 3 o bien 5 − 4x = −3

Despejando x :

Si 5 − 4x = 3

−4x = 3 − 5

−4x = −2    /−1

4x = 2

Si 5 − 4x = −3

−4x = −3 − 5

−4x = −8    /−1

4x = 8

Las soluciones para la ecuación primitiva son 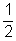 y 2 .
Conocida esta respuesta, podemos representar el conjunto solución de nuestra ecuación 3 |5 − 4x| = 9 a través de la notación de conjunto como:

Recuerde que un valor absoluto siempre es mayor o igual a cero, nunca negativo (  ).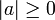

OBSERVA EL VÍDEO DE VALOR ABSOLUTO DE UN NUMERO REAL

LOS NUMEROS REALES

¿Qué son números reales?

Los números reales son todos aquellos números que se encuentran en la recta numérica y que conforman el grupo de números racionales e irracionales, negativos y positivos, incluyendo al número cero.

El sistema de números reales está formado principalmente por dos grandes grupos, el de los números racionales, que son todos aquellos números que pueden ser expresados como la división de dos números enteros, y el sistema de números irracionales cuya representación decimal es expansiva, infinita y no periódica. Los números racionales pueden ser también divididos en subgrupos, entre los cuales podemos mencionar: las fracciones no enteras con sus notaciones negativas; los números enteros incluyendo los números negativos y los enteros positivos; estos últimos a su vez incluyen a los números naturales y al cero.

Los números reales son dígitos que nos sirven para poder llevar a acabo todas las operaciones matemáticas necesarias para resolver una situación o problema. También tienen como función, designar la cantidad de elementos que tienen un conjunto determinado. Sirven para identificar lugares u objetos y para ordenar y jerarquizar categorías.

Entre las principales características de los números reales podemos mencionar las siguientes:

• Está formado por la unión de los números racionales y los irracionales.
• Son un conjunto completo.
• Este tipo de números y la recta numérica tienen una relación estrecha.
• Para cada número real existe un punto que lo representa dentro de la recta numérica.
• Los números naturales son completos y es un conjunto ordenado.
• Son números que tienen asociatividad y conmutatividad.
• Todos tienen un orden y se escriben en forma consecutiva.
• Cuando son utilizados para contar, entonces nos referimos a que tienen una función cardinal.

Los números reales se clasifican o dividen en los siguientes grupos:

• Números naturales: Estos son los números que normalmente utilizamos para contar. Pueden empezar con el 0 o con el 1. Sirven de base para formar números más grandes, y son números que poseen divisibilidad y distribución de números. Con ellos se puede sumar, restar, multiplicar y dividir.
• Números enteros: Son los números que pueden escribirse sin necesidad de utilizar una fracción. Son números completos y se utilizan para expresar cantidades, profundidades, temperaturas. Juntos, forman el grupo más pequeños de los números reales.
• Números racionales: Son los números que pueden ser expresados como fracción de dos números enteros, que tienen un numerador y un denominador. Se representa por medio de la letra Q. Pueden también ser definidos como tipos de equivalencias de pares enteros.
• Números irracionales: Son los números reales que no son tampoco números racionales. Estos números no pueden ser expresados como fracciones. Entre ellos podemos mencionar el radio de una circunferencia, el número áureo y la raíz cuadrada.

Las operaciones matemáticas que se pueden realizar utilizando números reales son: adición o suma, multiplicación, resta, división y potenciación.

Observa el vídeo  donde encontraras la clasificación de los números: naturales, enteros, racionales, irracionales, reales, complejos